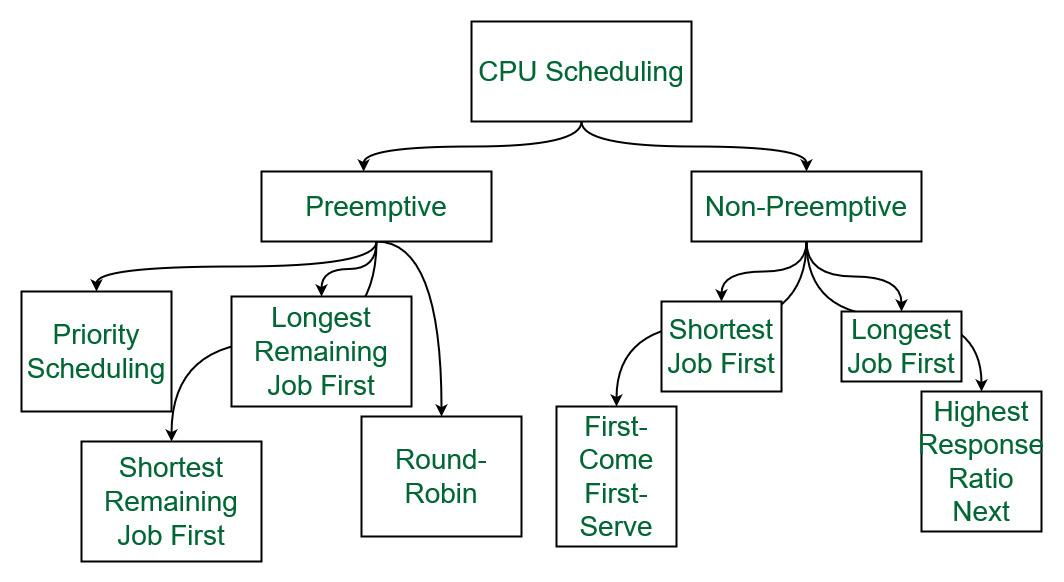
What is
CPU-Scheduling?
CPU scheduling, a critical component of process management, facilitates the efficient utilization of the CPU by allowing processes to execute while others are temporarily delayed due to resource unavailability such as I/O operations. Its primary objective is to ensure timely completion of tasks, enhancing system efficiency, speed, and fairness. When the CPU is idle, the operating system employs a temporary scheduler to select the next process from the queue of ready processes awaiting execution. This scheduler evaluates the readiness of each process in memory and allocates the CPU to the most suitable candidate, thereby optimizing resource utilization and overall system performance.
First Come First Serve
The simplest CPU scheduling algorithm, FCFS (First Come, First Serve), prioritizes processes based on their arrival times, utilizing a FIFO queue. As processes enter the ready queue, their PCBs are appended to the queue's tail. When the CPU becomes available, the process at the head of the queue is allocated the CPU and subsequently removed from the queue. FCFS can be either preemptive or non-preemptive, executing tasks in the order they arrive. While easy to implement, FCFS may result in high wait times and is less efficient, making it better suited for batch systems where longer process durations are tolerable.
So let's work on some examples from the given picture above and break it down bit by bit.
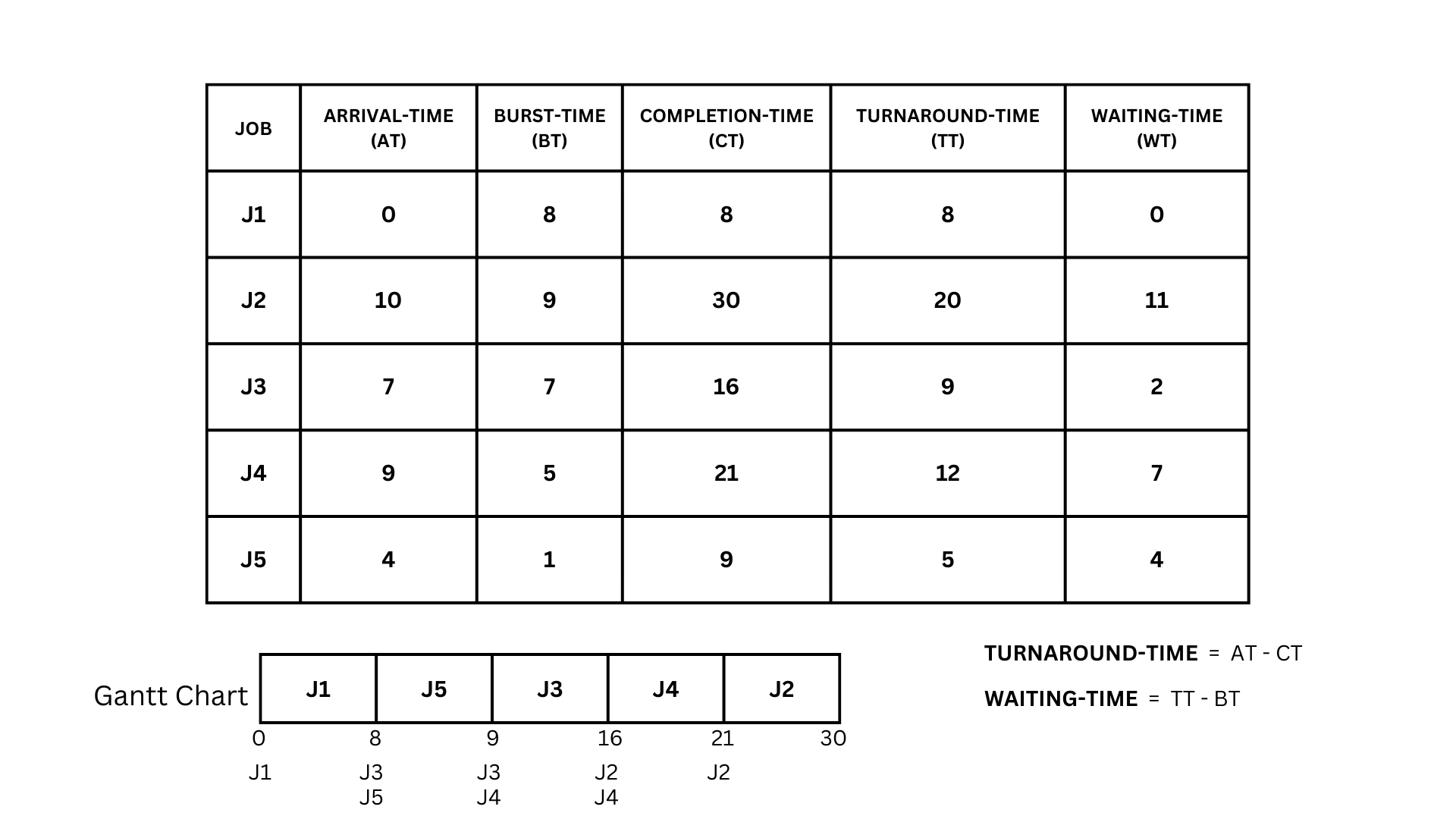
- The first would be to solve for the completion time, and this can be done by using a gantt chart. With both the arrival time and the given time, we could use that for the gantt chart.
- So using the arrival time of the processes, we have to process the one who came earlier, so it's going to be J1 as it's the one who came first with the arrival time of 0.
- Then we have to process the J1 with its burst time of 8.
- After we processed the first job, as you can see, we ended it at 8. Within those 8 came 2 jobs, which were J3 and J5, which have a burst time of 7 and 4, respectively.
- To know which one to process first in a queue of jobs in the First Come First Serve Algorithm we have to use the arrival time of the queued jobs.
- In this case we would process the J5 first because it arrived much earlier than the J3.
- Then we would use all of the burst time of J5, and the process ended at 9, then another job arrived, which is the j4.
- Using the same criteria we used earlier for multiple queued jobs, we would process the one who arrived first, which in this case is J3, which ended at 16. Inside those 16 then arrived another job, which is J2.
- Then we'll use the criteria again, which in this case is J4 because it arrived first than j2. After we processed J4, which ended at 21, no other job arrived, so we will process the remaining job, J2, which ended at 30.
- Now that our Gantt chart is done, we can now solve the remaining parts of the table, which are the turnaround time and waiting time.
- First would be the turnaround time, which we can solve by subtracting the completion time of the job from its arrival time.
- Now that we know the equation for the turnaround time, we can now calculate the turnaround time for each job.
- So we have J1, which has an arrival time of 0 and a completion time of 8. Using the formula for the turnaround-time (0-8), the answer would be 8. Now do the same for the others. J2 = (10 - 30 = 20), J3 = (7 - 16 = 9), J4 = ( 9 - 21 = 12), J5 = (4 - 9 = 5).
- Now that we got the turnaround-time of all of the jobs we can now calculate the waiting time of each job. This is done by subtracting the turnaround-time and the burst time of each jobs
- With that, let's calculate the waiting time for each job.
- For J1, we can see that it has a turnaround s of 8 and a burst time of 8. By subtracting those two, we get a 0 as an answer.Now lets do the rest of the jobs.
- For J2,it has a turnaround time of 20 and a burst time of 9 so J2 = (20 - 9 = 11)J3 = (9 - 7 = 2), j4 = (12 - 5 = 7), j5 = (5 - 1 =4)
- The calculations for the Average turnaround time are as follows: get the summation of turnaround time and divide the sum by how many items are there. In this case, the summation of turnaround time is 54 divided by 5, which gives us 10.8.
- Next is the average waiting time. It's just as simple: we're going to do the same thing as we did for the average turnaround time. so it will be the summation of Waiting time 24 divided by 5, which gives us 4.8 as the answer
- Now for the CPU utilization. In this one, we are going to need the sum of our burst time, divide it by our total completion time, and multiply it by 100. So in this case, the summation of burst time is 30; divide it by our end time, which is 30; then multiply by 100, we get a total of 100% CPU-Utilization.
Gantt Chart
Turnaround Time and Waiting Time
Turnaround-Time
Waiting Time
Average turnaround time, average waiting time, CPU Utilization
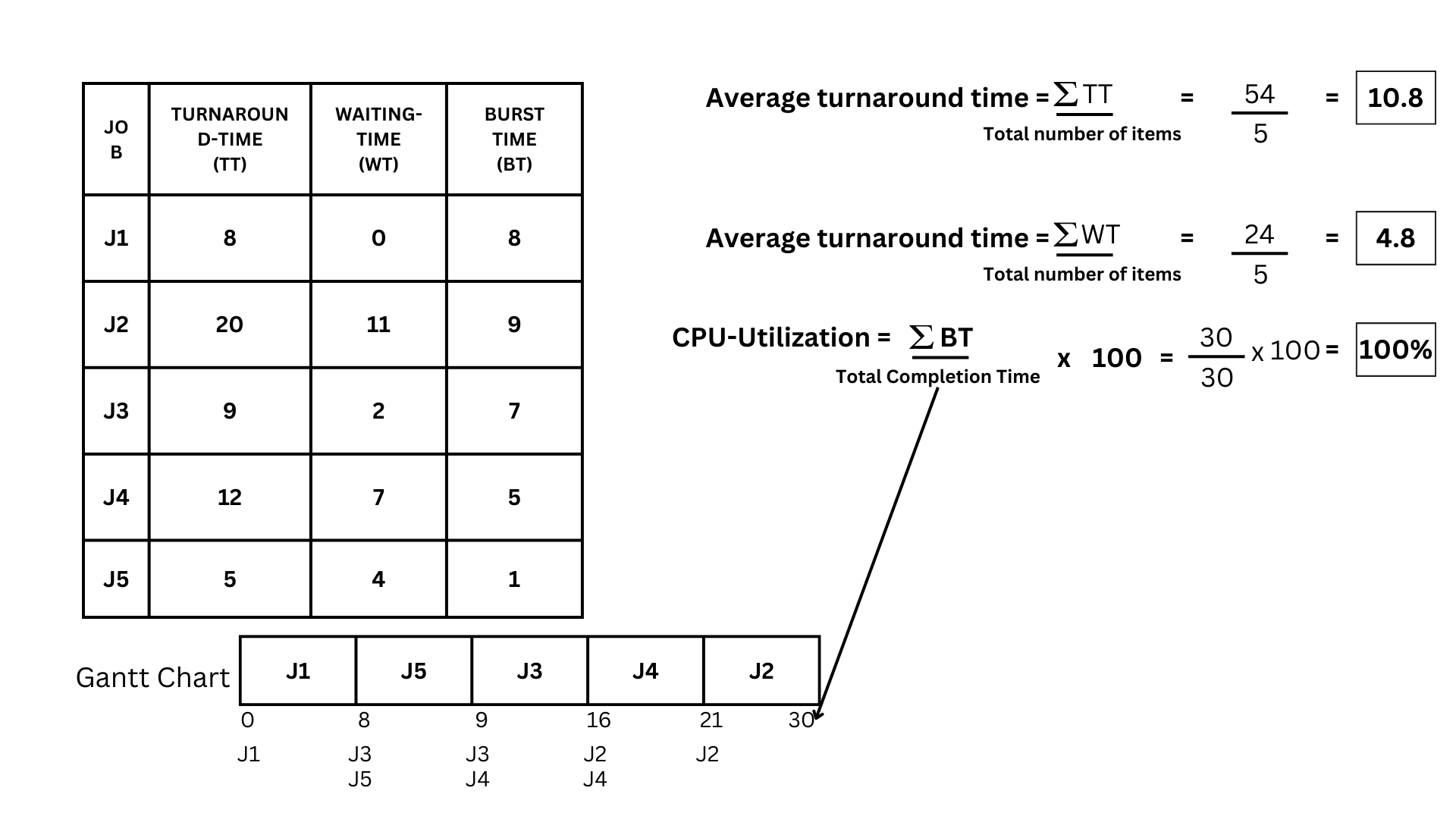
Average turnaround time
Shortest Job First
The Shortest Job First (SJF) or Shortest Job Next (SJN) is a scheduling policy that prioritizes the process with the smallest execution time. This can be either preemptive or non-preemptive. It’s a Greedy Algorithm known for its minimal average waiting time among all scheduling algorithms. However, it may lead to starvation if shorter processes continually arrive, which can be mitigated using the concept of ageing. While it’s practically challenging to implement as the Operating System may not know burst times, several methods, like a weighted average of previous execution times, can estimate a job’s execution time. This makes SJF suitable for specialized environments where accurate running time estimates are available. The algorithm works by sorting all processes according to their arrival time, then selecting the process with the minimum arrival and burst time. After a process is completed, a pool of processes that arrive afterward is created, and the process with the minimum burst time is selected from this pool.
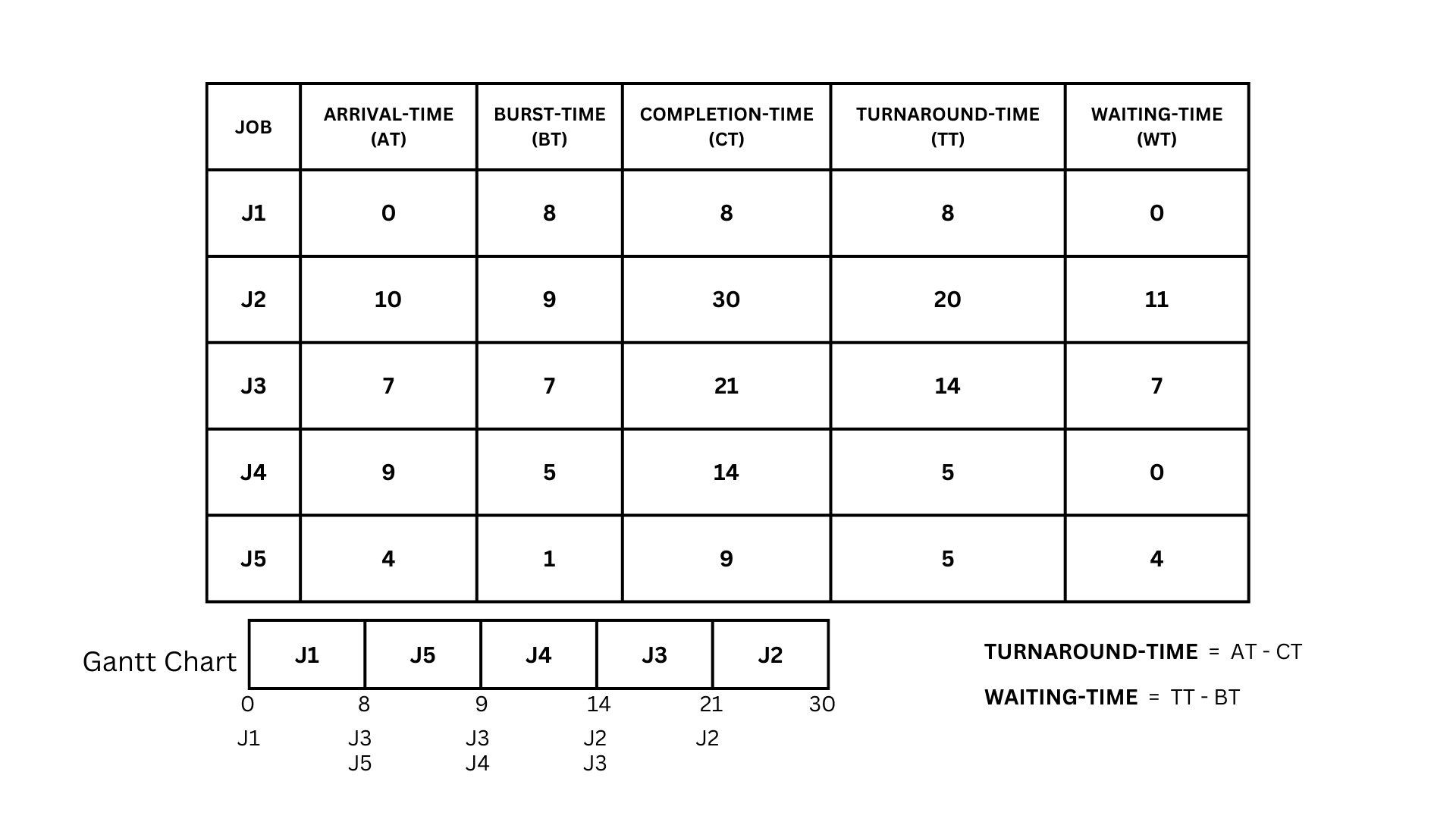
So let's work on some examples for Shortest Job First from the given picture above and break it down bit by bit.
- As we did in the first come, first serve algorithm, we would create a Gantt chart based on the arrival and burst time of our jobs.
- Although it's almost the same, it has a different way of doing its priority compared to the first come, first serve.
- Shortest Job First uses burst time to know which to process next if there are multiple jobs on the ram.
- So with that in mind we can now create a gantt chart for our Shortest Jobs First Algorithm.
- Back to the table, we can see that J1 arrived first and no other jobs are in the ram, so now we have to process j1 all the way.
- Now that we have a burst time of 8, J3 and J5 arrived.
- And now we can use the criteria for Shortest Job First, which is that when there are more than 1 process inside the ram, the one who will be processed first is the one with the lowest burst time.
- In this case, based on the table above, J5 has a lower burst time than J3, so J5 will be processed first. After we processed that we were at 9 m/s, another job arrived, which is the J4.
- So by utilizing the criteria again, we will process J4 first as it has a lower burst time than J3 in the queue ending at 14 then comes J2. Now we will process J3 as it has a lower burst time than j2ending at 21, and lastly, we will now process J2 and end at 30 m/s.
- Now that our Gantt chart is done, we can now solve the remaining parts of the table, which are the turnaround time and waiting time.
- First would be the turnaround time, which we can solve by subtracting the completion time of the job from its arrival time.
- Now that we know the equation for the turnaround time, we can now calculate the turnaround time for each job.
- So we have J1, which has an arrival time of 0 and a completion time of 8. Using the formula for the turnaround-time (0-8), the answer would be 8. Now do the same for the others. J2 = (10 - 30 = 20), J3 = (7 - 21 = 14), J4 = ( 9 - 14 = 5), J5 = (4 - 9 = 5).
- Now that we got the turnaround-time of all of the jobs we can now calculate the waiting time of each job. This is done by subtracting the turnaround-time and the burst time of each jobs
- With that, let's calculate the waiting time for each job.
- For J1, we can see that it has a turnaround time of 8 and a burst time of 8. By subtracting those two, we get a 0 as an answer.Now lets do the rest of the jobs.
- For J2,it has a turnaround time of 20 and a burst time of 9 so J2 = (20 - 9 = 11)J3 = (14 - 7 = 7), j4 = (5 - 5 = 0), j5 = (5 - 1 = 4)
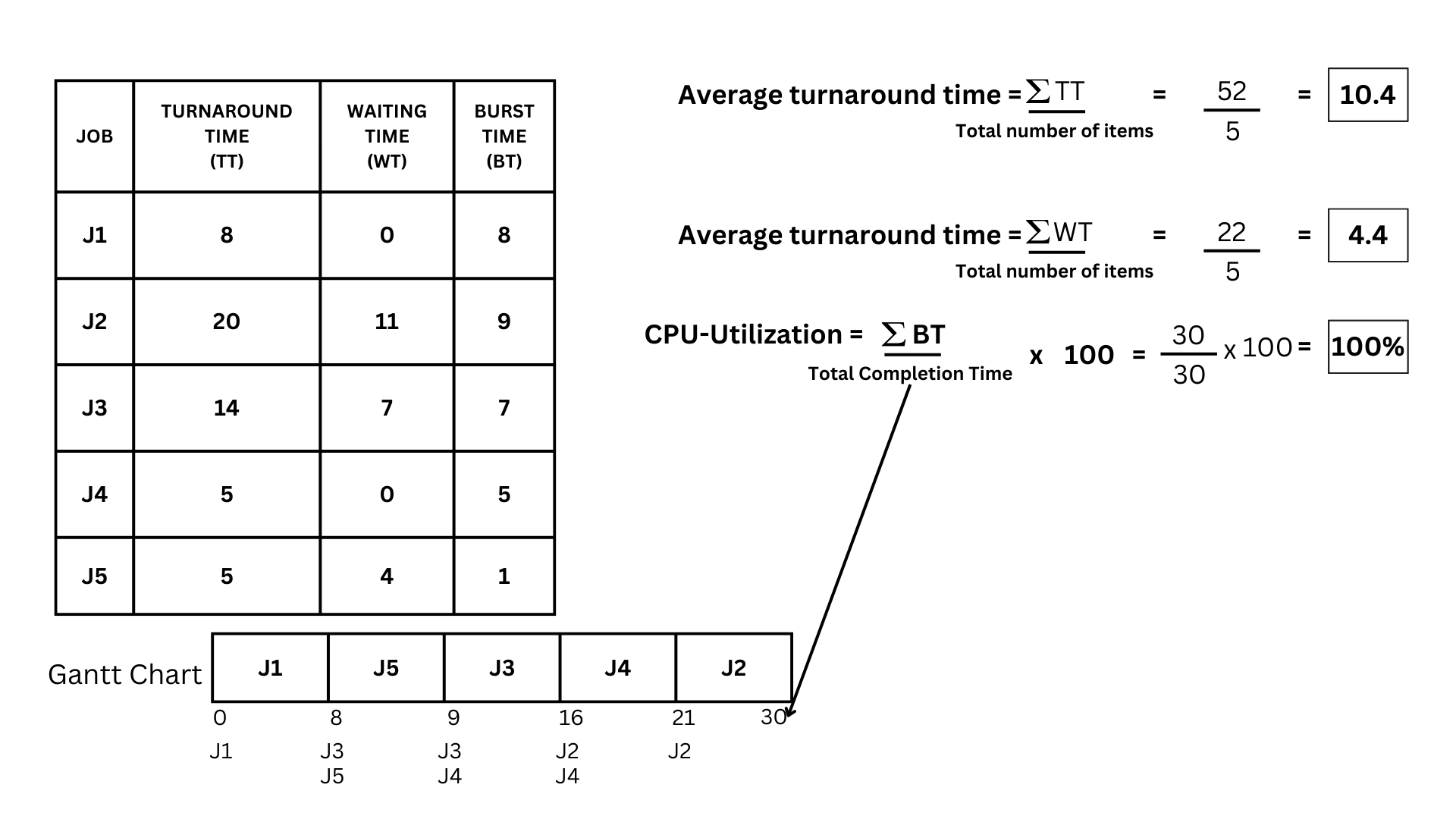
- The calculations for the Average turnaround time are as follows: get the summation of turnaround time and divide the sum by how many items are there. In this case, the summation of turnaround time is 52 divided by 5, which gives us 10.4.
- Next is the average waiting time. It's just as simple: we're going to do the same thing as we did for the average turnaround time. so it will be the summation of Waiting time 22 divided by 5, which gives us 4.4 as the answer
- Now for the CPU utilization. In this one, we are going to need the sum of our burst time, divide it by our total completion time, and multiply it by 100. So in this case, the summation of burst time is 30; divide it by our end time, which is 30; then multiply by 100, we get a total of 100% CPU-Utilization.
Gantt Chart
Turnaround Time and Waiting Time
Turnaround-Time
Waiting Time
Average turnaround time, average waiting time, CPU Utilization
Average turnaround time
Shortest Remaining Time First
The Shortest Remaining Time First (SRTF) is a preemptive version of the Shortest Job First (SJF) scheduling algorithm. Unlike SJF, which is non-preemptive and lets a process run to completion once started, SRTF can interrupt a running process if a new process with a shorter remaining time arrives. This leads to improved response times as shorter tasks get completed quickly. However, it also results in increased overhead due to frequent context switching and CPU time monitoring, unlike SJF which has less overhead but may not provide the best turnaround times for shorter tasks that arrive after a long task has started execution.
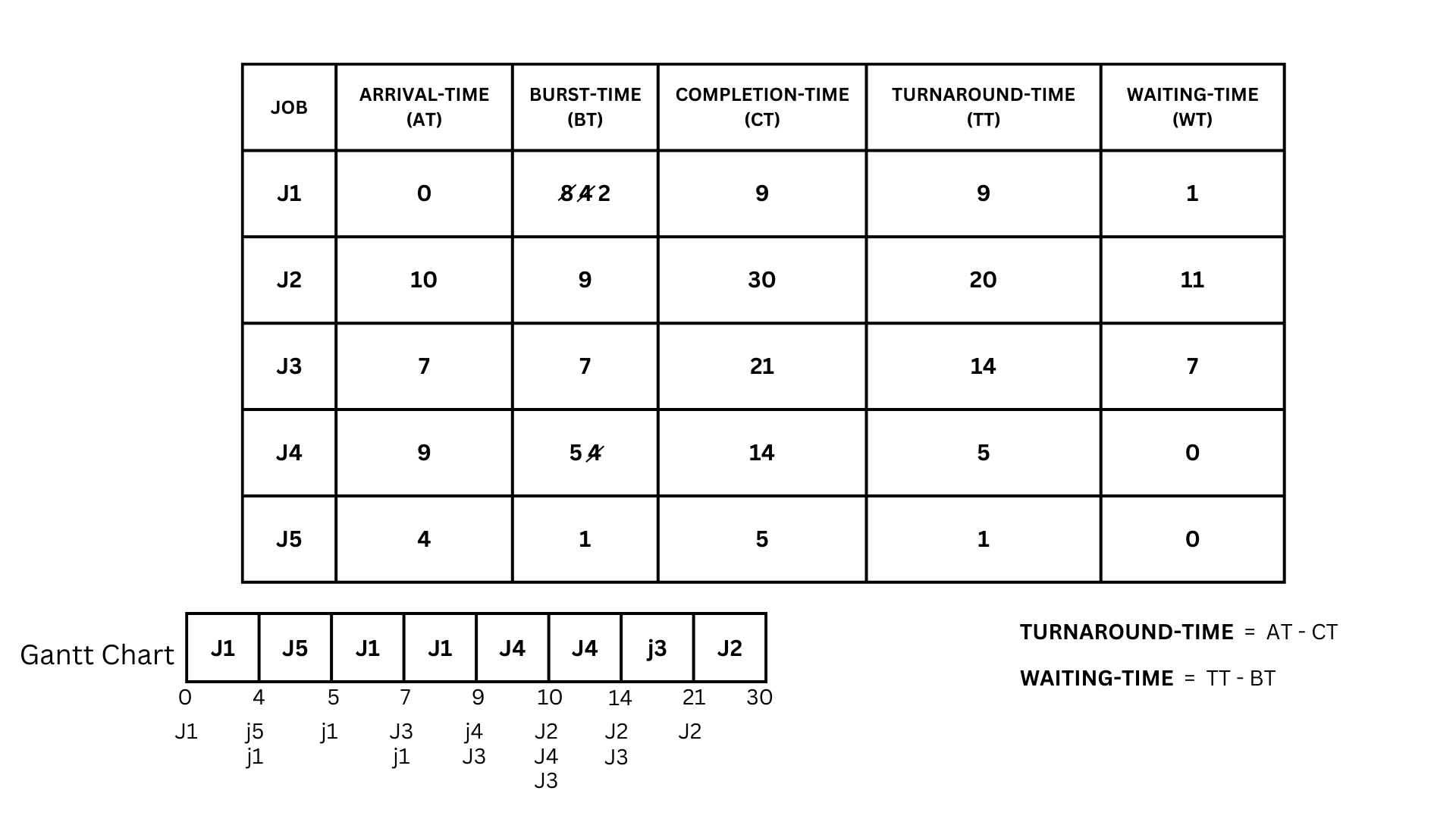
So let's work on some examples from the given picture above and break it down bit by bit.
- To make a gantt chart for the SRTF, or shortest remaining time first, it's basically the same as shortest job first; the only difference is that this scheduling algorithm is preemptive, meaning it has to stop processing the job if another job arrives while processing.
- Referring to the table above, we can see that J1 arrived first, so we will process it.
- Now, while it is processing, we can now use the rule for the shortest remaining time first algorithm, and that is, when a job arrives, the current job that is being processed will come to a halt.
- So now J1 will have to stop at time 4 because the job J5 arrived and we have to deduct the time used for J1 making its burst time 4.Now that we have a queue, we would now have to look at the burst time to see which job to process first, much like Shortest Job First.
- J5 has a lower burst time than J1, so we have to process it first. Using all of its burst time, we would stop at time 5, in which only J1 is in the queue. So we have to process J1 until time 7, deduct the 2 from its current burst time making it 2, and then another job arrives, which is J3.
- Again, we have multiple jobs in the queue, so we would have to check their burst time to see which is lower so that it can be processed first. In this case, it would be J1 as it has only two burst time left processing until time 9, at which time another job arrives, which is J4.
- We would have to process J4 first as it has a lower burst time than J3, We would only consume 1 of its burst time as another job arrives at time 10, which is J2.
- Now that we have all the processes in the ram and there are no more jobs to arrive, we can now consume all of the burst time of the remaining jobs in the queue without stopping the process.
- Using the criteria again, we can check each of their burst times to know which to process. First, we will have to process J4 and consume its remaining time, which is 4, ending its process at time 14. Next is J3, which has a burst time of 7, ending at time 21, and lastly, the remaining job, which is J2, with a burst time of 9, ending at time 30.
- Now that our Gantt chart is done, we can now solve the remaining parts of the table, which are the turnaround time and waiting time.
- First would be the turnaround time, which we can solve by subtracting the completion time of the job from its arrival time.
- Now that we know the equation for the turnaround time, we can now calculate the turnaround time for each job.
- So we have J1, which has an arrival time of 0 and a completion time of 9. Using the formula for the turnaround-time (0-9), the answer would be 9. Now do the same for the others. J2 = (10 - 30 = 20), J3 = (7 - 21 = 14), J4 = ( 9 - 14 = 5), J5 = (4 - 5 = 1).
- Now that we got the turnaround-time of all of the jobs we can now calculate the waiting time of each job. This is done by subtracting the turnaround-time and the burst time of each jobs
- With that, let's calculate the waiting time for each job.
- For J1, we can see that it has a turnaround time of 9 and a burst time of 8. By subtracting those two, we get a 1 as an answer.Now lets do the rest of the jobs.
- For J2,it has a turnaround time of 20 and a burst time of 9 so J2 = (20 - 9 = 11)J3 = (14 - 7 = 7), j4 = (5 - 5 = 0), j5 = (1 - 1 = 0)
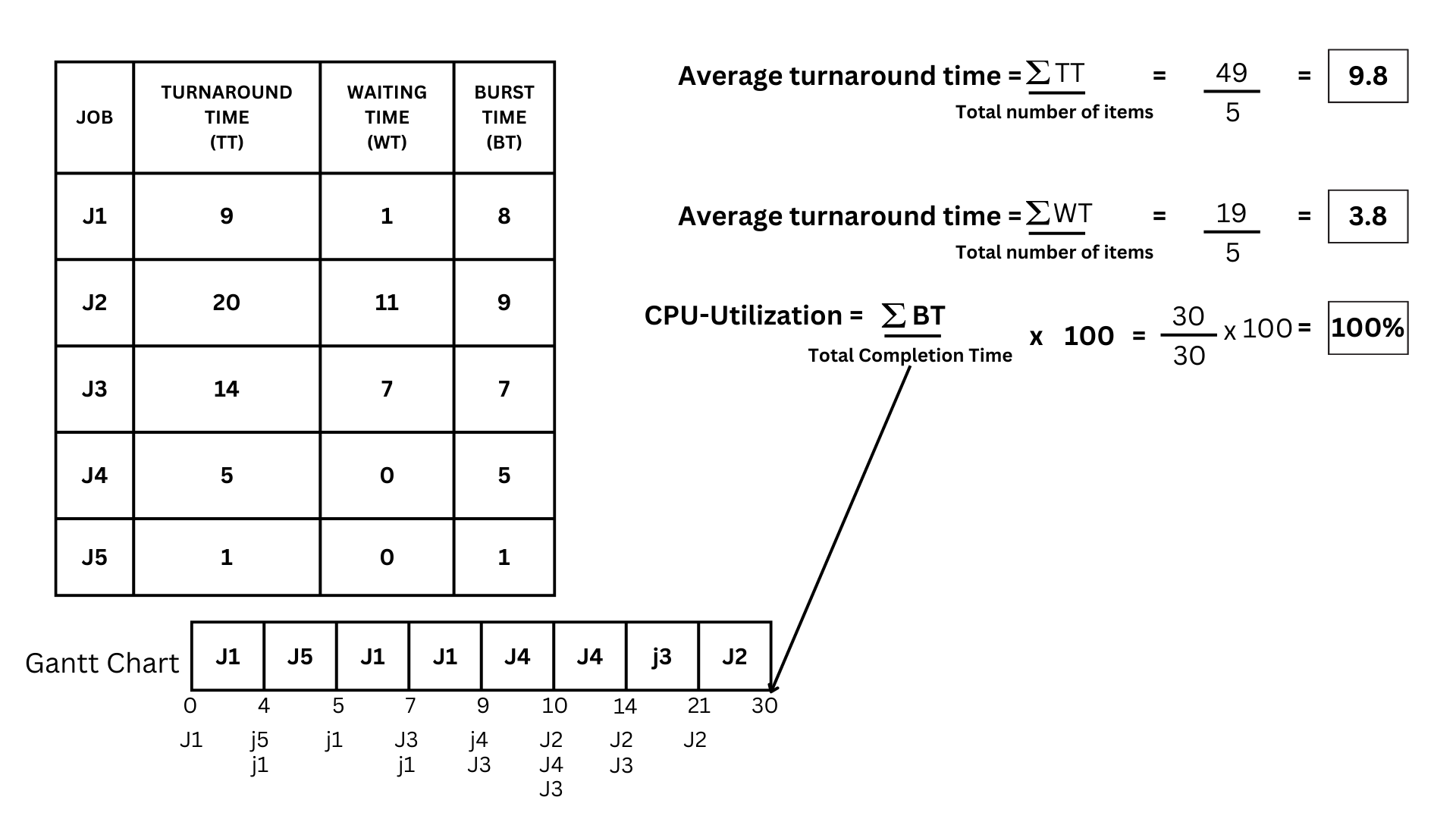
- The calculations for the Average turnaround time are as follows: get the summation of turnaround time and divide the sum by how many items are there. In this case, the summation of turnaround time is 49 divided by 5, which gives us 9.8.
- Next is the average waiting time. It's just as simple: we're going to do the same thing as we did for the average turnaround time. so it will be the summation of Waiting time 19 divided by 5, which gives us 3.8 as the answer
- Now for the CPU utilization. In this one, we are going to need the sum of our burst time, divide it by our total completion time, and multiply it by 100. So in this case, the summation of burst time is 30; divide it by our end time, which is 30; then multiply by 100, we get a total of 100% CPU-Utilization.
Gantt Chart
Turnaround Time and Waiting Time
Turnaround-Time
Waiting Time
Average turnaround time, average waiting time, CPU Utilization
Average turnaround time
Priority(Preemptive)
The Preemptive Priority CPU Scheduling Algorithm is a method that prioritizes tasks based on their rank, with lower-ranking processes having higher priority. In the event of a conflict where multiple processes have the same priority, it defaults to a First Come, First Serve (FCFS) approach. The algorithm begins by selecting the first process with an arrival time of zero. It then checks the priority of the next available process, executing the one with a higher priority. If the priorities are equal, it executes the process that arrived first. This process is repeated until all processes have been executed, always choosing the highest priority process at each step. This ensures that tasks are executed efficiently and in order of their importance.
Furthermore, in preemptive priority CPU scheduling, a running process can be interrupted by a higher-priority process. If a process with a higher priority arrives, the currently running process is suspended, and the higher priority process is executed. If the preempted process still has CPU burst time left, it is then added back to the ready queue and waits for its next opportunity to run. This dynamic nature of preemptive scheduling allows it to quickly respond to changes in process priority, ensuring efficient use of CPU resources.
So let's work on some examples from the given picture above and break it down bit by bit.
- So the same as the non-preemptive priority algorithm, the job that arrives at time 0 is J1, but we would only process J1 until time 4 because another job will arrive at that time, so from 8 J1's burst time was reduced to 4 as we used a part of its burst time. That's the rule for the preemptive priority algorithm.
- Now at time 4, a job arrives, which is J5. Now that we have multiple jobs at the ram, we have to check their priority to know which one is supposed to be processed first. J5 has a higher priority than J1, so we would process that first until time 5, because it only has a burst time of 1.
- We would process J1 again as it is the only job in the queue, but only until time 7 as another job arrived, which is J3. Now just reduce the used burst time for the current burst time of J1, and that leaves us with a burst time of 2.
- Now that we have multiple jobs in the queue again, we will look at their priority to see which one to process first. J3 has a higher priority than J1, so we would process J3 first until time 9 as another job arrives, which is J4.
- Again, look at their priorities and check which one has the highest priority over the other; in this case, J3 still has the higher priority than the two, so we would process J3 first only until time 10, at which point J2 arrives.
- As we can see at the table, no other jobs will arrive anymore, so now we can use all of their remaining burst time without stopping.
- Checking their burst time again, we can process J3 first as it has a higher priority. Using all of its remaining burst time, we would end at time 14.
- Next would be J2, as it has a higher priority, ending at time 23, then J1, ending at time 25, and finally J4, ending at time 30.
- Now that our Gantt chart is done, we can now solve the remaining parts of the table, which are the turnaround time and waiting time.
- First would be the turnaround time, which we can solve by subtracting the completion time of the job from its arrival time.
- Now that we know the equation for the turnaround time, we can now calculate the turnaround time for each job.
- So we have J1, which has an arrival time of 0 and a completion time of 25. Using the formula for the turnaround-time (0-25), the answer would be 25. Now do the same for the others. J2 = (10 - 23 = 13), J3 = (7 - 14 = 7), J4 = ( 9 - 30 = 21), J5 = (4 - 5 = 1).
- Now that we got the turnaround-time of all of the jobs we can now calculate the waiting time of each job. This is done by subtracting the turnaround-time and the burst time of each jobs
- With that, let's calculate the waiting time for each job.
- For J1, we can see that it has a turnaround time of 25 and a burst time of 8. By subtracting those two, we get a 17 as an answer.Now lets do the rest of the jobs.
- For J2,it has a turnaround time of 13 and a burst time of 9 so J2 = (13 - 9 = 4)J3 = (7 - 7 = 0), j4 = (21 - 5 = 16), j5 = (1 - 1 = 0)
- The calculations for the Average turnaround time are as follows: get the summation of turnaround time and divide the sum by how many items are there. In this case, the summation of turnaround time is 67 divided by 5, which gives us 13.4.
- Next is the average waiting time. It's just as simple: we're going to do the same thing as we did for the average turnaround time. so it will be the summation of Waiting time 37 divided by 5, which gives us 7.4 as the answer
- Now for the CPU utilization. In this one, we are going to need the sum of our burst time, divide it by our total completion time, and multiply it by 100. So in this case, the summation of burst time is 30; divide it by our end time, which is 30; then multiply by 100, we get a total of 100% CPU-Utilization.
Gantt Chart
Turnaround Time and Waiting Time
Turnaround-Time
Waiting Time
Average turnaround time, average waiting time, CPU Utilization
Average turnaround time
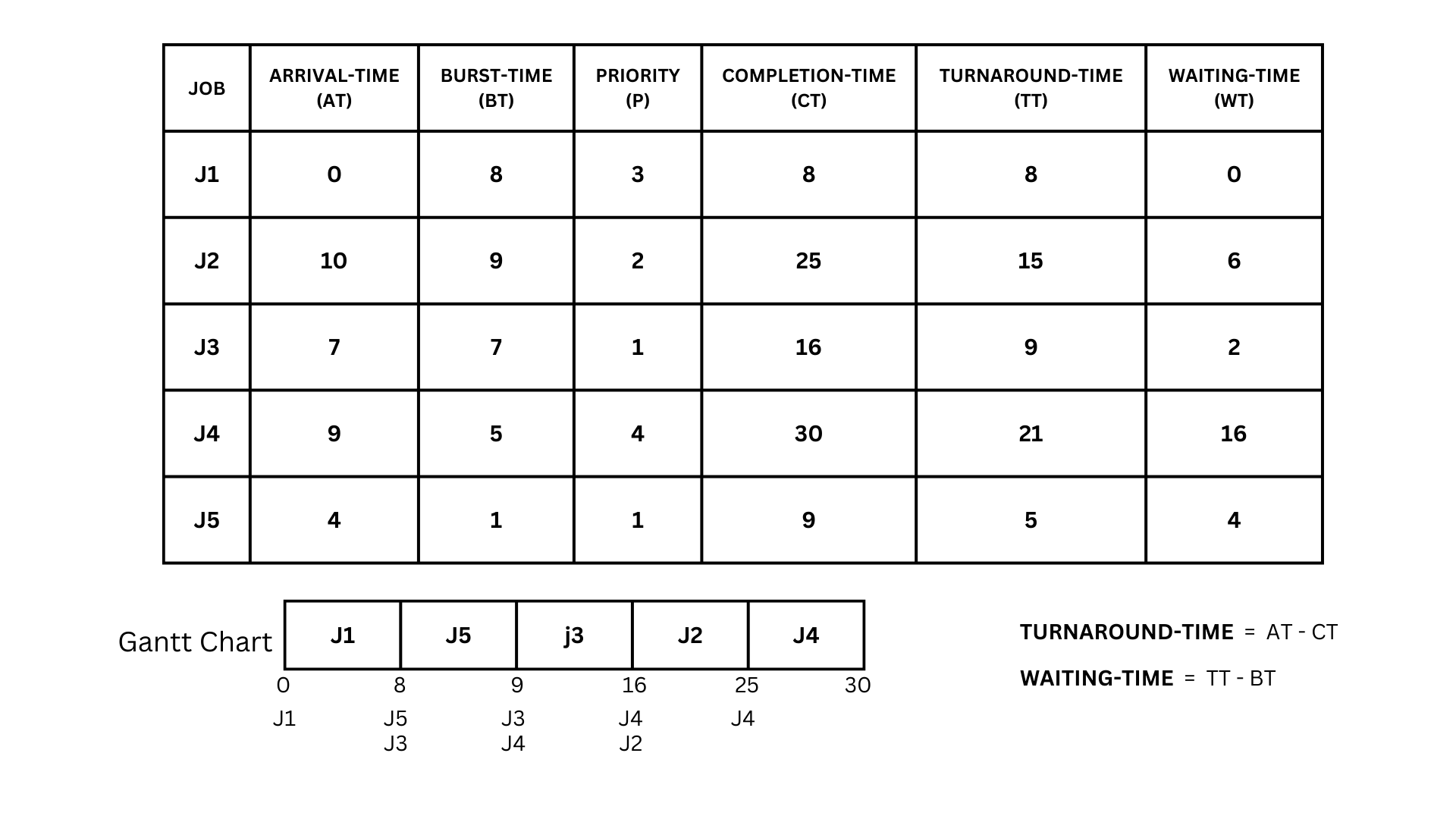
Priority(Non-Preemptive)
Priority scheduling is a non-preemptive algorithm commonly used in batch systems. It operates by assigning each process an arrival time and priority, with the first process scheduled being the one with the lowest arrival time. If multiple processes share the same arrival time, the one with the highest priority is scheduled first. If two processes have the same priority, the one with the lower process number is scheduled first. This process continues until all processes have been executed. It’s important to note that the priority number’s significance (whether a lower or higher number indicates a higher priority) will be clearly stated in the question. Once all processes have arrived, they can be scheduled based on their priority. This approach ensures efficient and fair process scheduling.

So let's work on some examples from the given picture above and break it down bit by bit.
- The first job to arrive at the queue is J1, so we have to process all of its burst time. That ends at time 8, and within that time, two jobs arrive at the queue, which are J5 and J3.
- Now that we have multiple jobs in the queue, we will have to use the criteria for priority, which states that we have to process the one who has a higher priority than the others, with 1 being the highest priority.
- So back to the example, we can see two jobs in the queue, J5 and J3. J5 has a priority number of 1, and J3 has the same priority number, 1. To break the tie between the two, we would look at the next criteria, which is the burst time. The lower the burst time, the higher the priority to be processed, the same as the Shortest Job First Scheduling Algorithm.
- So in this case, we would process J5 first, as it has a lower burst time than J3. After we processed J5, we arrived at time 9, where another job arrived, which was J4.
- Again, we have multiple jobs in the queue, so we would use the criteria for the priority scheduling algorithm to know which one to process first. As we can see in the table above, J3 has a priority number of 1 and J4 has a priority number of 4, so we would have to process J3 first as it has a higher priority value than J4, ending its burst time at time 16; another job arrived, which is J2.
- J2 has a priority number of 2 and J4 has a priority number of 4, so we will have to process J2 first, ending its burst time at time 25, and finally processing the final job in the queue, which is J4, ending its burst time at time 30.
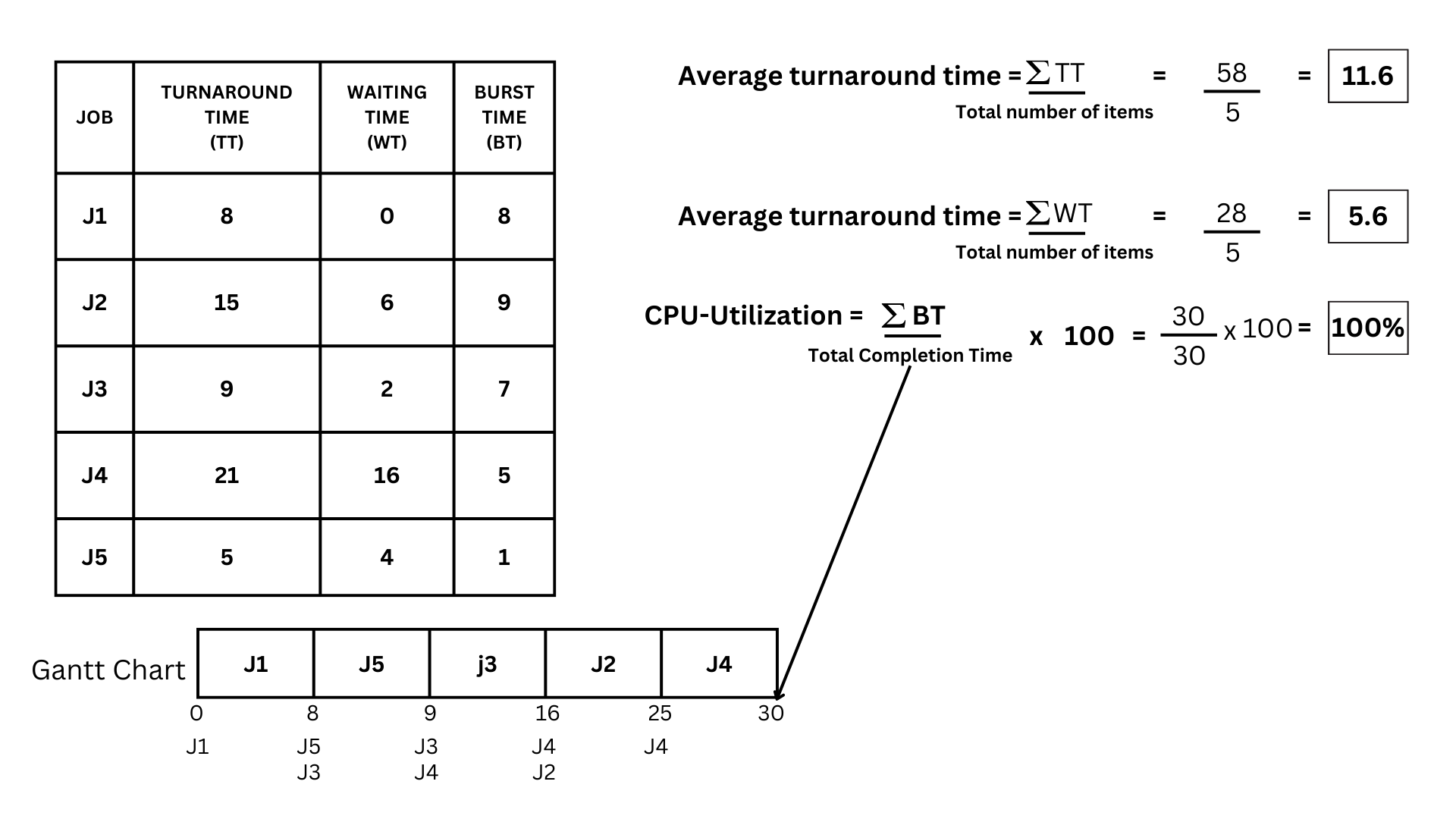
- Now that our Gantt chart is done, we can now solve the remaining parts of the table, which are the turnaround time and waiting time.
- First would be the turnaround time, which we can solve by subtracting the completion time of the job from its arrival time.
- Now that we know the equation for the turnaround time, we can now calculate the turnaround time for each job.
- So we have J1, which has an arrival time of 0 and a completion time of 8. Using the formula for the turnaround-time (0-8), the answer would be 8. Now do the same for the others. J2 = (10 - 25 = 15), J3 = (7 - 16 = 9), J4 = ( 9 - 30 = 21), J5 = (4 - 9 = 5).
- Now that we got the turnaround-time of all of the jobs we can now calculate the waiting time of each job. This is done by subtracting the turnaround-time and the burst time of each jobs
- With that, let's calculate the waiting time for each job.
- For J1, we can see that it has a turnaround time of 8 and a burst time of 8. By subtracting those two, we get a 0 as an answer.Now lets do the rest of the jobs.
- For J2,it has a turnaround time of 20 and a burst time of 9 so J2 = (15 - 9 = 6)J3 = (9 - 7 = 2), j4 = (21 - 5 = 16), j5 = (5 - 1 = 4)
- The calculations for the Average turnaround time are as follows: get the summation of turnaround time and divide the sum by how many items are there. In this case, the summation of turnaround time is 58 divided by 5, which gives us 11.6.
- Next is the average waiting time. It's just as simple: we're going to do the same thing as we did for the average turnaround time. so it will be the summation of Waiting time 28 divided by 5, which gives us 5.6 as the answer
- Now for the CPU utilization. In this one, we are going to need the sum of our burst time, divide it by our total completion time, and multiply it by 100. So in this case, the summation of burst time is 30; divide it by our end time, which is 30; then multiply by 100, we get a total of 100% CPU-Utilization.
Gantt Chart
Turnaround Time and Waiting Time
Turnaround-Time
Waiting Time
Average turnaround time, average waiting time, CPU Utilization

Average turnaround time
Round Robin
The Round Robin CPU scheduling algorithm is a preemptive version of the First Come First Serve algorithm, where each process is assigned a fixed time slot in a cyclical manner. This algorithm, which focuses on time-sharing techniques, allows each process in the ready queue to be assigned the CPU for a specific time quantum. If a process completes its execution within this time, it ends; otherwise, it returns to the waiting table for its next turn. The Round Robin algorithm is simple, easy to implement, and starvation-free, ensuring fairness as each process gets an equal share of the CPU. However, it has the disadvantage of increased context switching overhead, larger waiting and response times, low throughput, and potentially large Gantt charts if the quantum time is small. Despite these drawbacks, it remains one of the most commonly used techniques in CPU scheduling.
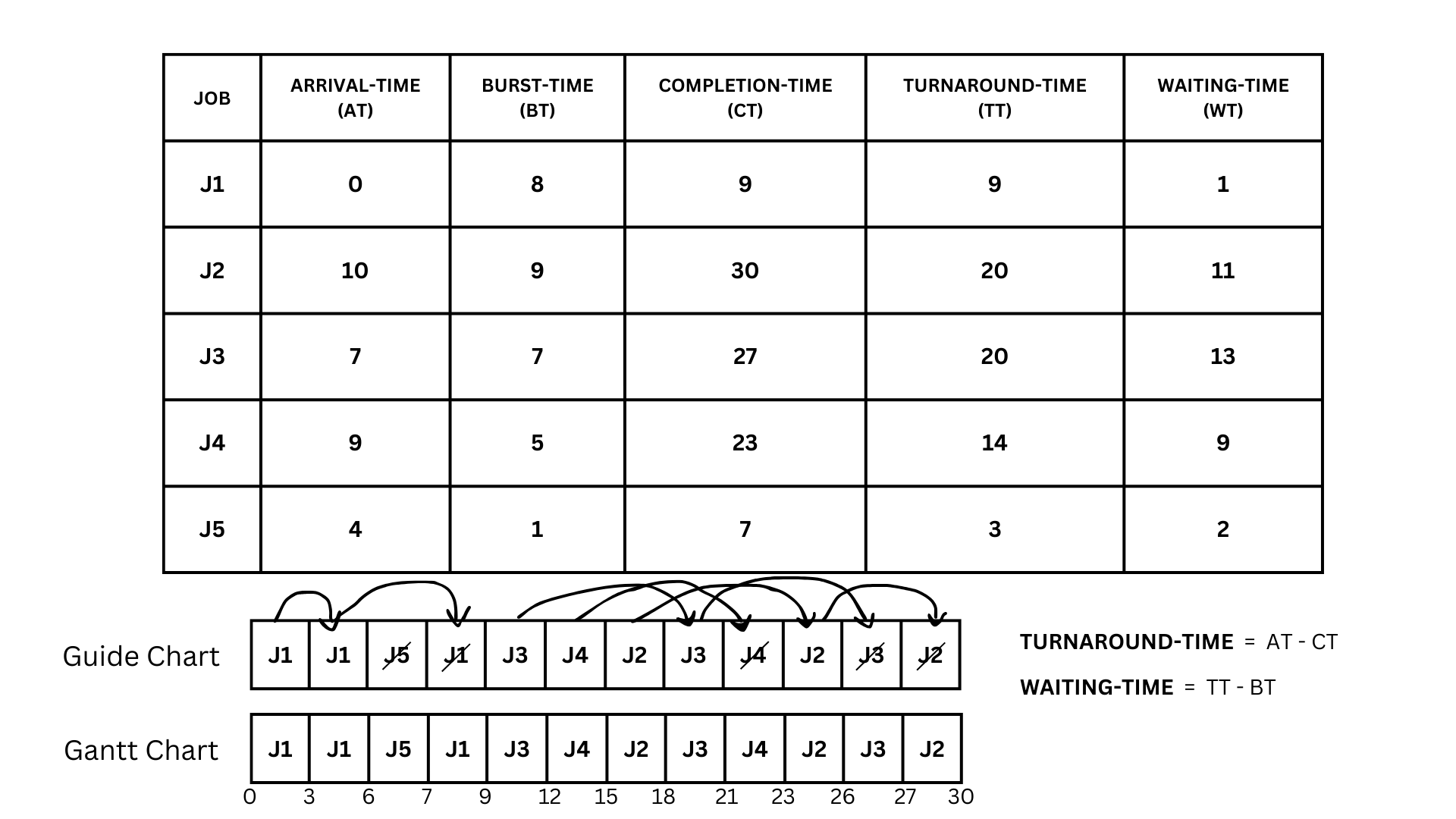
So let's work on some examples from the given picture above and break it down bit by bit.
- First, we need to create a Gantt chart. Given the quantum of 3, each job will be processed for a maximum of 3 units at a time.
- We start with J1 as it arrives first at time 0. We process it for 3 units (the quantum), so it ends at time 3 and goes back to the end of the queue with a remaining burst time of 5.
- Next, we have J5 which arrived at time 4. Since no other jobs have arrived between time 3 and 4, the CPU is idle for 1 unit. We then process J5 for 1 unit (its total burst time), so it ends at time 5.
- At time 5, both J1 and J3 are in the queue. But J1 arrived earlier, so we process it next for 3 units. It ends at time 8 with a remaining burst time of 2.
- Next, we process J3 for 3 units. It ends at time 11 with a remaining burst time of 4.
- At time 11, J1, J4, and J2 are in the queue. We process J1 first as it arrived earlier. It ends at time 13 and is now complete.
- We then process J4 for 3 units. It ends at time 16 with a remaining burst time of 2.
- Next, we process J2 for 3 units. It ends at time 19 with a remaining burst time of 6.
- We then process J3 for 3 units. It ends at time 22 with a remaining burst time of 1.
- Next, we process J4 for 2 units. It ends at time 24 and is now complete.
- We then process J2 for 3 units. It ends at time 27 with a remaining burst time of 3.
- Next, we process J3 for 1 unit. It ends at time 28 and is now complete.
- Finally, we process J2 for 3 units. It ends at time 31 and is now complete.
- Now that our Gantt chart is done, we can now solve the remaining parts of the table, which are the turnaround time and waiting time.
- First would be the turnaround time, which we can solve by subtracting the completion time of the job from its arrival time.
- Now that we know the equation for the turnaround time, we can now calculate the turnaround time for each job.
- So we have J1, which has an arrival time of 0 and a completion time of 9. Using the formula for the turnaround-time (0-9), the answer would be 9. Now do the same for the others. J2 = (10 - 30 = 20), J3 = (7 - 27 = 20), J4 = ( 9 - 23 = 14), J5 = (4 - 7 = 3).
- Now that we got the turnaround-time of all of the jobs we can now calculate the waiting time of each job. This is done by subtracting the turnaround-time and the burst time of each jobs
- With that, let's calculate the waiting time for each job.
- For J1, we can see that it has a turnaround time of 9 and a burst time of 8. By subtracting those two, we get a 1 as an answer.Now lets do the rest of the jobs.
- For J2,it has a turnaround time of 20 and a burst time of 9 so J2 = (20 - 9 = 11)J3 = (7 - 20 = 13), j4 = (14 - 5 = 9), j5 = (1 - 3 = 2)
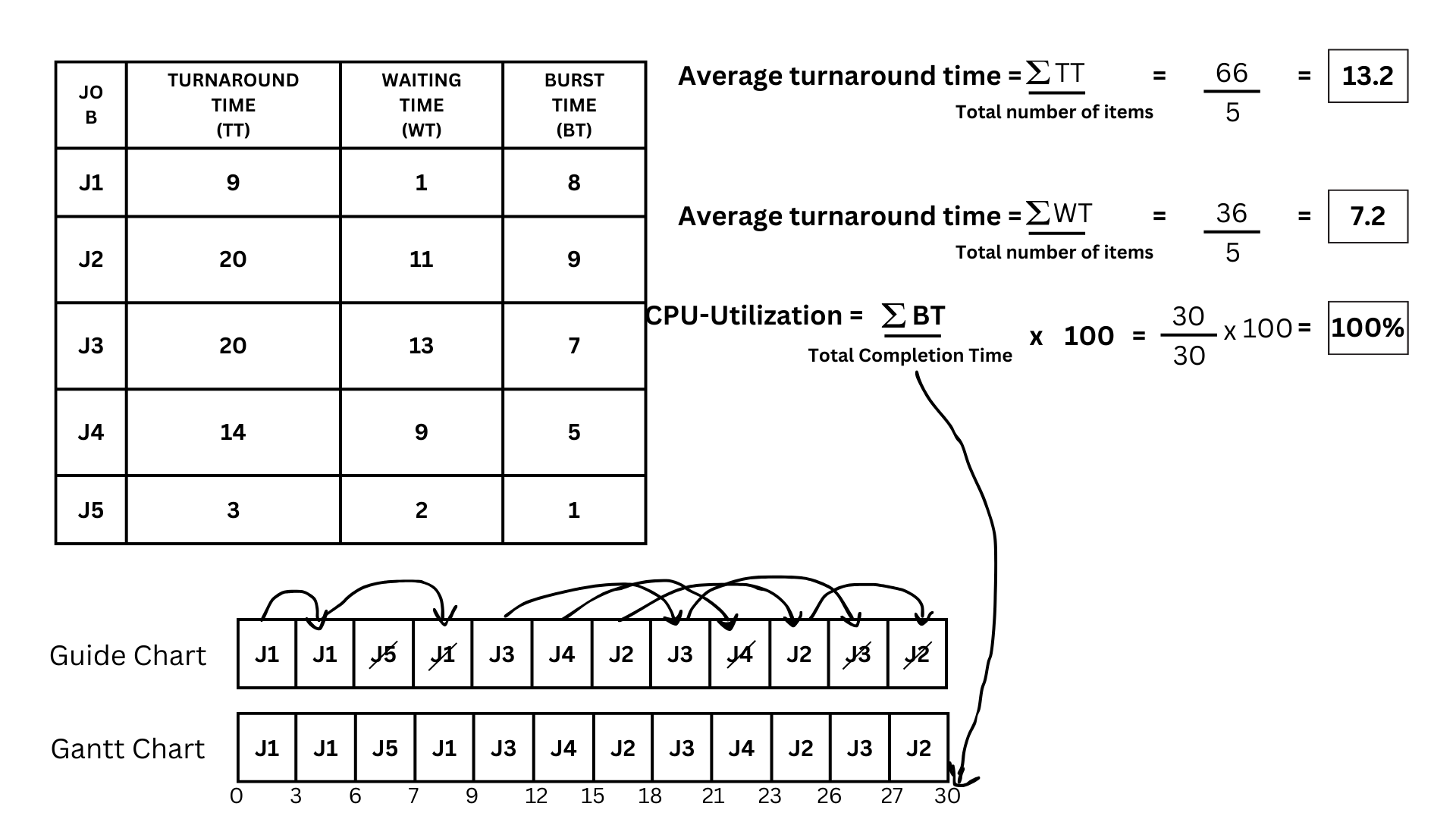
- The calculations for the Average turnaround time are as follows: get the summation of turnaround time and divide the sum by how many items are there. In this case, the summation of turnaround time is 66 divided by 5, which gives us 13.2.
- Next is the average waiting time. It's just as simple: we're going to do the same thing as we did for the average turnaround time. so it will be the summation of Waiting time 36 divided by 5, which gives us 7.2 as the answer
- Now for the CPU utilization. In this one, we are going to need the sum of our burst time, divide it by our total completion time, and multiply it by 100. So in this case, the summation of burst time is 30; divide it by our end time, which is 30; then multiply by 100, we get a total of 100% CPU-Utilization.
Gantt Chart
Turnaround Time and Waiting Time
Turnaround-Time
Waiting Time
Average turnaround time, average waiting time, CPU Utilization